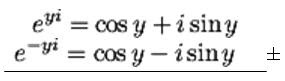Ini adalah materi lanjutan dari "Bilangan Kompleks...(ii) {Dalil De Moivre}"... Mohon dilihat kembali untuk lebih jelasnya.. ^^.. Dan ini mungkin bisa dikatakan sebagai materi yang rumit bagi kebanyakan mahasiswa di universitasku.. Namun sesungguhnya, kita tidak perlu menjadi profesor untuk membuktikan rumus *dewa* ini, karena bukti itu sekarang sudah jelas di depan mata, dan lagi *bukti ini cukup mudah diturunkan*!!
=========================================================================
PROOF
Bukti ini banyak makan tempat.. Oleh karena itu, saya menggunakan banyak singkatan atau permisalan:
Ingat konsep awal euler bahwa:
Dengan melihat konsep itu, cobalah untuk menguraikan bentuk
. = 
= 
Ingat-ingat kembali.. z jika dinotasikan dalam polar adalah sebagai berikut.
z = [mod.(z)] . cis[arg(z)]
Lalu, ingatlah dalil De Moivre yang bunyinya berikut.
Oleh karena itu, dapat dikatakan bahwa:
Kita tulis ulang dalam bentuk x dan y, maka menjadi:
Lanjuutt. Tadi, kita sudah sampai sini...z = [mod.(z)] . cis[arg(z)]
Lalu, ingatlah dalil De Moivre yang bunyinya berikut.
Oleh karena itu, dapat dikatakan bahwa:
Kita tulis ulang dalam bentuk x dan y, maka menjadi:
= Kita beri notasi mod. untuk kedua ruas.
= 
= 
= 
Kita dapatkan persamaan berikut:
= <----- diambil dari ruas paling kiri dan kanan. Lalu, kita buat n mendekati tak hingga (agar bisa sesuai dengan konsep awal, konsep euler).
=
=
=
=
= <----- diambil dari ruas paling kiri dan kanan. Jika ditulis ulang menjadi:
Ingat-ingat kembali.. z jika dinotasikan dalam polar adalah sebagai berikut.
z = [mod.(z)] . cis[arg(z)]
Lalu, ingatlah dalil De Moivre yang bunyinya berikut.
Oleh karena itu, dapat dikatakan bahwa:
Kita tulis ulang dalam bentuk x dan y, maka menjadi:
z = [mod.(z)] . cis[arg(z)]
Lalu, ingatlah dalil De Moivre yang bunyinya berikut.
Oleh karena itu, dapat dikatakan bahwa:
Kita tulis ulang dalam bentuk x dan y, maka menjadi:
Nah, kita kembali ke persamaan awal, yaitu persamaan di bawah:
= Kita beri notasi arg. untuk kedua ruas.
= 
= 
Kita dapatkan persamaan berikut:
= <---------- diambil dari ruas paling kiri dan kanan.. Dekati n hingga tak terhingga (agar sesuai dengan konsep awal, konsep euler). 
= 
=
= 
Oleh karena itu:
= <----- diambil ruas yang paling kiri dan kanan. Jika ditulis ulang menjadi:
Kita sudah mendapatkan 
dan 
. Selanjutnya, kita kembali ke konsep awal.
Substitusikan dan , maka menjadi:
dan . Selanjutnya, kita kembali ke konsep awal. dan , maka menjadi:
Terbukti
=========================================================================
KEADAAN KHUSUS
Jika x=0, maka persamaan eulernya menjadi:
... (i)Seandainya y negatif, maka:
... (ii)Lalu, kita lakukan operasi penjumlahan atau pengurangan pada kedua persamaan:
*)
*)
=========================================================================
Ternyata, pembuktian persamaan euler ini cukup mudah.. Hanya memakai konsep limit saja sudah cukup. Tidak perlu mengunakan pengintegralan dan sebagainya...
Btw, ada yang mo nanya gakk?? ayo.. ayoo.. nanya.. mumpung gratisss.. ^^
Lihat juga lanjutan post ini: Variabel Kompleks(iv){Review}.. ^^
Sumber: Kalkulus I (Wikaria Gazali), dosen tercinta di Universitas Bina Nusantara
