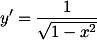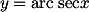BUKTI DASAR TURUNAN DERIVATIF

BUKTI DASAR TURUNAN DERIVATIF

8:05 AM
Berikut adalah rumus-rumus dasar turunan/ derivatif:
Bila y=f(x) , y'=f'(x), dan a adalah konstanta maka:
1.
2.




3.
4.
_
5.




6.



etc...
Lihat lanjutan post di bawah untuk mengetahui bukti-buktinya.
=========================================================================
Mengapa Turunan dari  adalah ?? (a konstanta)
Bukti ini sangat mudah. Langsung kita gunakan definisi dari derivatif.
 (atau bisa kita gunakan cara seperti di post "bukti sifat-sifat turunan" yang dilakukan secara bertahap..)
.







TERBUKTI
Selanjutnya: Mengapa turunan dari  adalah ??
Kita bisa saja menguraikan penurunan rumus ini dari awal, seperti cara yang serupa seperti di atas. Namun, kita gunakan saja rumus sebelumnya, untuk membuktikan rumus ini., supaya kita tidak 2 kali kerja..

Di atas merupakah rumus yang sudah kita dapatkan sebelumnya. Substitusikan a=e.
Ingat bahwa ln e =1. Ingat bahwa:  = , maka:
TERBUKTI
=========================================================================
Mengapa turunan dari  adalah  ??
ln-kan kedua ruas.
turunkan kedua ruas. Ingat bahwa turunan dari ln x adalah 1/x.

TERBUKTI
=========================================================================
Mengapa turunan dari  adalah ?? (a konstanta)
ln-kan kedua ruas.
turunkan kedua ruas, maka hasilnya:
TERBUKTI
Selanjutnya: Mengapa turunan dari  adalah ??
Sesuai dengan rumus sebelumnya:
Jika a=e, maka:


TERBUKTI
=========================================================================
Mengapa turunan dari  adalah ??
Untuk membuktikan ini, kita bisa gunakan definisi awal dari derivatif.
.
Ingat bahwa: 
==> Note: rumus di atas HARUS dapat diturunkan sendiri.
Dengan demikian, persamaan  menjadi:


TERBUKTI
Mengapa turunan dari  adalah  ??
Pembuktiannya menggunakan cara yang sama seperti di atas.

Ingat bahwa: 
==> rumus di atas HARUS bisa diturunkan sendiri.
Dengan demikian, persamaan  menjadi:





TERBUKTI

Note: Cara lain menurunkan turunan sin x dan cos x yaitu dengan melihat identitas eulernya (Lihat disini):
*) 
*) 
Dengan menurunkan sisi ruas kanan dari , maka akan menghasilkan sisi kanan dari .
Mengapa turunan dari  adalah ??
Fungsi tangen dapat dibentuk ke dalam bentuk pembagian.

Kemudian, ingatlah sifat turunan berikut.

Dengan menggunakan sifat itu, maka pembuktian turunan f(x) akan segera terbukti.




TERBUKTI

Rumus-rumus di atas adalah rumus turunan yang siap pakai. Selanjutnya, akan dibahas pembuktian untuk rumus-rumus yang kurang begitu *terpakai*. Jika terpakai pun, kita dapat dengan mudah menurunkannya. Konsep menurunkannya sama seperti di atas, kecuali adanya beberapa yang mengharuskan substitusi trigonometri.. But, lagi-lagi, rumus di bawah jangan sengaja dihapal (kecuali kalau tidak sengaja terhapal).. ;P

Bukti: turunan dari , , dan 
Bukti bisa menggunakan teorema sebelumnya yang berbunyi: .
Sama halnya seperti menggunakan dalil rantai...



Dengan aturan rantai, maka:
 

 
TERBUKTI
Bukti turunan dari fungsi arcsin x, arccos x, arctan x, etc
Tidak semua bukti akan diberikan di sini, karena prosesnya hampir sama. Dan, akan terlalu banyak jika semuanya dibahas dalam satu post di blog. So, it is your challenge to prove it by yourself...

Bukti turunan dari fungsi arcsin x
Turunkan kedua ruas, maka hasilnya:
Dengan menggambar segitiga siku-siku dengan sudut y (memisalkan sisi depan adalah x, sisi miring 1), maka kita akan mendapatkan cos y. (Lihat gambar)
Atau, kita bisa memanfaatkan identitas trigonometri: , maka:
.
Di sini, kita dapat: . Maka, tinggal disubstitusikan...

TERBUKTI
Bukti turunan dari fungsi arccotan x

Turunkan kedua ruas maka hasilnya:


, maka .
Gambarkan segitiga siku-siku dengan sudut y. Misalkan sisi depan adalah 1, dan sisi samping adalah x. (lihat gambar).
Dengan demikian, kita bisa menghitung panjang sisi miring, kemudian menghitung nilai dari sin y.
Substitusikan nilai dari sin y ke persamaan sebelumnya.


TERBUKTI
Bukti turunan dari fungsi hiperbolik: sinh x, cosh x, etc

Pembuktiannya menggunakan sisi kanan dari identitas terhadap euler. Ingat bahwa:



Bukti turunan sinh x
 (TERBUKTI)

Bukti turunan cosh x
 (TERBUKTI)

Bukti turunan tanh x

___________ (TERBUKTI)

=========================================================================
Masih banyak bukti yang belum dibuktikan karena keterbatasan waktu.. Namun, prosesnya tidak berbeda jauh seperti pembuktian di atas.. Jika ada yang merasa kesulitan, silakan bertanya di comment.. ^^
sumber
Deby

Share this

More

Related Posts

Next
« Prev Post
Previous
Next Post »

:)
:(
hihi
:-)
:D
=D
:-d
;(
;-(
@-)
:P
:o
:>)
(o)
:p
:-?
(p)
:-s
(m)
8-)
:-t
:-b
b-(
:-#
=p~
$-)
(y)
(f)
x-)
(k)
(h)
cheer
Subscribe to: Post Comments (Atom)